Challenge 2: Directed Graph Supersource
- 14 minsIn order to follow along with this problem and my solution, the reader should be familiar with Directed Graphs.
Overview
Definitions
Adjacency Matrix
An Adjacency Matrix is a way to encode a directed graph in a matrix storing binary values.
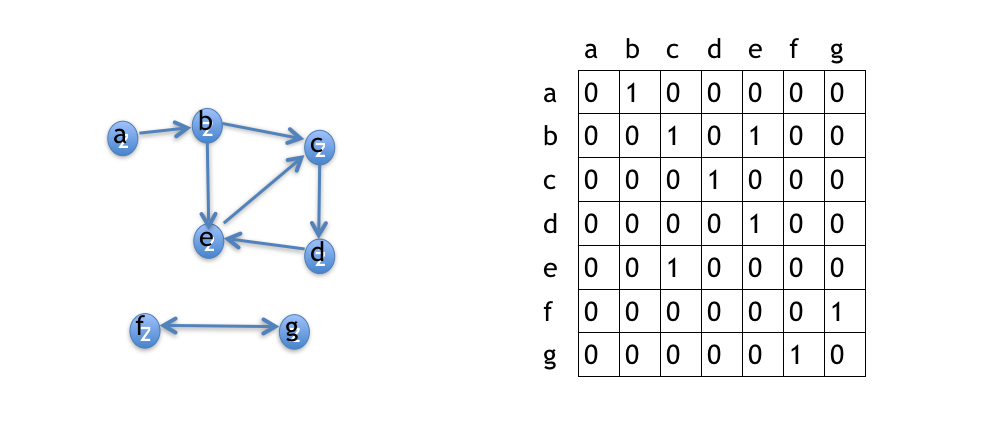
A one represents an edge from the node represented by the row, to the node in the column. A zero represents no edge between two nodes.
Supersource
We say that a node \(u\) of a directed graph \(G = (V, E)\) is a supersource, if there is an edge from \(u\) to every other node in \(G\) and there is no edge from any node into \(u\), i.e., for all \(v \neq u ∈ V ,\:\: (u, v) ∈ E\) and for all \(v ∈ V ,\:\: (v, u) \notin E\).
Challenge
Suppose the directed graph \(G = (V, E)\) is given by its adjacency matrix \(A\).
(a)
Using pseudo-code, describe an efficient algorithm that acts on \(A\) to determine whether \(G\) has a supersource node, and if so, to output it.
Your algorithm should minimize the number of accesses to the adjacency matrix \(A\) in the worst-case (e.g., reading an arbitrary element \(A[i, j]\) of \(A\) counts as one access to \(A\)).
(b)
Prove your algorithm correct. It is convenient to assume that the set of nodes of \(G\) is \(V = {1,2,...,n}\).
My Solution
Let the set of nodes of \(G\) be \(V = \{1,2,...,n\}\).
Let each element in the adjacency matrix be accessed by using the number of the edge’s initial node to index the row, and by using the number of the edge’s terminal node to index the column.
In the Python-like pseudocode to follow, we will assume that arrays and matrices are 1-indexed. So for example, an array \(F\) with 4 spaces is indexed by the values \(\{1, 2, 3, 4\}\).
(a)
FIND_SUPERSOURCE(A):
""" Return the index of the supersource node in graph represented by
adjacency matrix A, or null if no supersource exists.
"""
B = [1] * n # Create an array of n 1's.
for i in range(1, n+1):
if B[i] == 1:
if ROW_IS_FILLED(A, B, i):
for j in range(1, n+1):
if A[j,i] == 1:
return null;
return i;
return null;
ROW_IS_FILLED(A, B, i):
""" Returns true if all elements in row i of matrix A are 1's,
or false if row i contains a 0.
"""
for j in range(1, n+1):
if j != i:
if A[i, j] == 1:
B[j] = 0;
else:
return false;
return true;(b)
To prove \(\text{FIND_SUPERSOURCE}\) correct, we must show that \(\exists \text{ supersource } u \rightarrow \text{ FIND_SUPERSOURCE(A) returns index of } u\) \(\land \:\: \nexists \text{ supersource } u \rightarrow \text{FIND_SUPERSOURCE(A) returns null}\).
From the definition of a supersource, we know that if there exists a supersource \(u\), then \(\forall x \neq u ∈ V ,\:\: (u, x) ∈ E\).
Thus, Lemma 1: if there exists a supersource \(u \in [1, n]\), then the adjacency matrix elements \([u, j] = 1 \:\: \forall j \in \{ 1, 2, ..., u-1, u+1, ..., n\}\).
We also know that, if there exists a supersource \(u\), there is no edge from any node into \(u\), or \(\forall x ∈ V ,\:\: (x, u) \notin E\).
Thus, Lemma 2: if there exists a supersource \(u \in [1, n]\), then the adjacency matrix elements \([i, u] = 0 \:\: \forall i \in \{1, ..., n\}\).
Case 1: Assume there exists a supersource \(u\) in the graph \(G\).
Then via Lemma 2 we know that there exists no \(i \in [1, n]\) for which \(A[i, u] = 1\). Thus for any call of \(\text{ROW_IS_FILLED}\) with \(B\) and any \(i \in [1,n]\), the lines of code
if A[i, u] == 1:
B[u] = 0;will never assign the index of the supersource to 0 in the list \(B\).
Taken with the knowledge that all elements of the array \(B\) are initialized to 1, this allows us to guarantee that in the following \(\text{FIND_SUPERSOURCE}\) loop, when \(i = u\), \(B[u] == 1\) will always evaluate to true regardless of what has happened before it, and thus \(\text{ROW_IS_FILLED}(A,B,u)\) is guaranteed to be called.
for i in range(1, n+1):
if B[i] == 1:
if ROW_IS_FILLED(A, B, i):Let us now examine the \(\text{ROW_IS_FILLED}\) pseudocode, and consider what happens when it is called with \(i\) as the number of the supersource. From Lemma 1, given supersource \(u\), we know that \(A[u, x] = 1 \:\: \forall x \in \{ 1, 2, ..., u-1, u+1, ..., n\}\). So we know that, when \(i\) is the index of the supersource, there exists no value of \(j \in [1, n]\) for which the code block
if j != i:
if A[i, j] == 1:
B[j] = 0;
else:
return false;returns false. Thus the entire loop
for j in range(1, n+1):
if j != i:
if A[i, j] == 1:
B[j] = 0;
else:
return false;executes without returning false, and thus \(\text{ROW_IS_FILLED}(A, B, i=u)\) returns true on the last line.
We have shown that on the iteration where \(i\) is the index of the supersource, \(\text{ROW_IS_FILLED}\) will be called and will return true. Thus the innermost loop in \(\text{FIND_SUPERSOURCE}\) executes with \(i\) as the index of the supersource.
for j in range(1, n+1):
if A[j,i] == 1:
return null;Via Lemma 2, we know that given supersource \(u\), the adjacency matrix elements \([i, u] = 0 \:\: \forall i \in \{1, ..., n\}\). Thus for no value of \(j \in [1, n]\) will \(A[j,i] = 1\). So all iterations of the loop pass without returning null. Then, referencing the pseudocode for \(\text{FIND_SUPERSOURCE}\), we can see that following the complete execution of the above loop without returning null, the index \(i\) of the supersource is returned.
Thus we have shown that \(\exists \text{ supersource } u \rightarrow \text{ FIND_SUPERSOURCE(A) returns index of } u\).
Case 2: Now, assume there is no supersource in the graph \(G\).
Then it is true that either (i) no node in \(G\) has an edge from it to every other node in \(G\), or (ii) there exists one or more nodes in \(G\) that have an edge from it to every other node in \(G\) but that also is a terminal node for one or more edges.
Case 2 (i): Let us assume that (i) is true. Then no node in \(G\) has an edge from it to every other node in \(G\). In terms of the adjacency matrix \(A\), this means that \(\forall i \in [1,n], \:\: \exists j \in \{1,...,i-1,i+1,...,n\} \text{ for which } A[i,j] == 0\).
Lemma 3: \(( \exists j \in \{1,...,i-1,i+1,...,n\}\) for which \(A[i,j] == 0 ) \rightarrow ( \text{ROW_IS_FILLED}(A, B, i)\) will reach at least one value of \(j\) in which the loop
for j in range(1, n+1):
if j != i:
if A[i, j] == 1:
B[j] = 0;
else:
return false;will return false \()\).
Via Lemma 3, under assumption (i) all calls of \(\text{ROW_IS_FILLED}\) on \(A\) within \(\text{FIND_SUPERSOURCE}\), which happen with values of \(i\) ranging from 1 to n, will return false, and \(\text{FIND_SUPERSOURCE}\) will return null on the last line.
Thus, in the case 2 (i) where there is no supersource in \(G\), and no node in \(G\) has an edge from it to every other node in \(G\), it has been shown that \(\text{FIND_SUPERSOURCE}\) will return null, as required.
Case 2 (ii): Now assume that (ii) is true - there exists at least one node \(x\) in \(G\) that has an edge from it to every other node in \(G\) but that also is a terminal node for at least one edge.
Correct behaviour of \(\text{FIND_SUPERSOURCE}\) under our assumption that there is no supersource in \(G\) requires all iterations of the main loop execute without returning an integer in the innermost loop.
Via Lemma 3, we can see that when the main loop of \(\text{FIND_SUPERSOURCE}\) calls \(\text{ROW_IS_FILLED}\) with any \(i\) representing a node in \(G\) that does not have directed edges into every other node, \(\text{ROW_IS_FILLED}\) returns false and the inner loop does not execute.
Thus the only iteration of the main loop of \(\text{FIND_SUPERSOURCE}\) that we must further examine under conditions of our assumption is when \(i = x\).
Case 2 (ii A): It may be that \(\exists \:\: y\) < \(x \in V\) such that \((y,x) \in E\). In this case, the loop
for i in range(1, n+1):
if B[i] == 1:
if ROW_IS_FILLED(A, B, i):will result in \(\text{ROW_IS_FILLED}(A,B,i=y)\) being called prior to \(i\) reaching the value of \(x\). When this happens, the edge \(A[y,x] == 1\) will mean that when \(j = x\), the following block of code assigns \(B[x] = 0\).
for j in range(1, n+1):
if j != i:
if A[i, j] == 1:
B[j] = 0;The effect of this is that when, in the main loop of \(\text{FIND_SUPERSOURCE, } i=x\), the lines of code
if B[x] == 1:
if ROW_IS_FILLED(A, B, x):simply bypass calling \(\text{ROW_IS_FILLED}(A, B, i=x)\), as \(x\) has already been eliminated as a possible supersource for having a edge leading into it.
Thus the all calls of \(\text{ROW_IS_FILLED}\) that occur in case 2 (ii A) are covered under Lemma 3 and will return false, and thus \(\text{FIND_SUPERSOURCE}\) will return null on the last line, as required.
Thus, in the case 2 (ii A), where there is no supersource in \(G\), and there exists at least one node \(x\) in \(G\) that has an edge from it to every other node in \(G\) but that also is a terminal node for at least one edge, and where \(\exists y\) < \(x \in V\) such that \((y,x) \in E\), it has been shown that \(\text{FIND_SUPERSOURCE}\) will return null, as required.
Case 2 (ii B): In the case that no nodes \(y\) with a directed edge into a node \(x\) have an index that is smaller than the index of \(x\), then
if B[x] == 1:
if ROW_IS_FILLED(A, B, x):will end up calling \(\text{ROW_IS_FILLED}(A, B, i=x)\).
Recall by our assumptions that node \(x\) has an edge leading from it to every other node in \(G\). This means that \(A[x, j] = 1 \:\: \forall j \in \{ 1, ..., x-1, x+1, ..., n\}\), so there exists no value of \(j \in [1, n]\) for which the code block
if j != i:
if A[i, j] == 1:
B[j] = 0;
else:
return false;returns false. Thus the entire loop
for j in range(1, n+1):
if j != i:
if A[i, j] == 1:
B[j] = 0;
else:
return false;executes without returning false, and thus \(\text{ROW_IS_FILLED}(A, B, i=x)\) returns true, and \(\text{FIND_SUPERSOURCE}\) moves on to execute the innermost loop.
Recall that by our assumption, \(x\) is also a terminal node for one or more edges. This means that \(\exists i \in \{1,..,x-1,x+1,...,n\}\) for which \(A[i,x] == 1\). This means that there exists some value of \(j\) for which the following loop returns null.
for j in range(1, n+1):
if A[j,i] == 1:
return null;Thus, in the case 2 (ii B) where there is no supersource in \(G\), but there exists at least one node \(x\) in \(G\) that has an edge from it to every other node in \(G\) but that also is a terminal node for at least one edge, and where no nodes \(y\) with a directed edge into a node \(x\) have an index that is smaller than the index of \(x\), it has been shown that \(\text{FIND_SUPERSOURCE}\) will return null, as required.
Having dealt with both case 2 (ii A) and case 2 (ii B), we have shown that in the general case 2 (ii) where there is no supersource in \(G\), and there exists at least one node \(x\) in \(G\) that has an edge from it to every other node in \(G\) but that also is a terminal node for at least one edge, \(\text{FIND_SUPERSOURCE}(A)\) will return null, as required.
Taking both case 2 (i) and 2 (ii) together, we have successfully demonstrated that \(\nexists \text{ supersource } u \rightarrow \text{FIND_SUPERSOURCE(A) returns null}\).
We have now successfully shown that \(\exists \text{ supersource } u \rightarrow \text{ FIND_SUPERSOURCE(A) returns index of } u\) \(\land \:\: \nexists \text{ supersource } u \rightarrow \text{FIND_SUPERSOURCE(A) returns null}\).
Thus, we have proven \(\text{FIND_SUPERSOURCE}\) to be correct.
